An n × n matrix A is diagonalizable if there is a matrix V and a diagonal matrix D such that A = VDV − 1. This happens if and only if A has n eigenvectors which constitute a basis for Cn. In this case, V can be chosen to be the matrix with the n eigenvectors as columns, and a square root of A is
 can be diagonalized as VDV − 1, where
can be diagonalized as VDV − 1, where  and
and  .
.
D has principal square root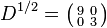 , giving the square root
, giving the square root 
 can be diagonalized as VDV − 1, where
can be diagonalized as VDV − 1, where  and
and  .
.D has principal square root
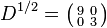 , giving the square root
, giving the square root 
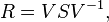

ليست هناك تعليقات:
إرسال تعليق