سلام عليكم: الموضوع ده يا شباب فكرت اكتبه لأن بعض الالعاب بتتلعب فى اوروبا وامريكا بس او حتى فى كوريا وفى العاب زى سيلك روود الكورى والروسى بيعرفوا من الاى بى بتاعك انك من مصر ويبندولك الأكونت...طيب الطريقة دى اسمها طريقة البروكسى تقدر تغير بيها الاى بى بتاعك مش بس كده ده كمان هتختار الاى بى يكون من اى بلد فى العالم. ندخل على الشرح : أول حاجة كليك يمين بالفارة على ايكونة انترنت اكسبلور الموجودة على سطح المكتب يظهر لك المربع ده زى اللى فى الصورة تختار منه properties  بعد كده هيظهرلك النافذة اللى فى الصورة  هتختار منها connectionsوهيظهر لك الصفحة دى  بعد كده تضغط على lan setting هيظهر لك النافذه دى هتعلم صح فيها امام use aproxy server for your lan  بعد كده هتدخل على عنوان الرابط التالى ip-adress.com/proxy_list هتظهر لك صفحة مليانة ارقام اى بى لناس من دول العالم كله وامام كل اى بى علم الدولة....هتختار رقم الاى بى للدولة اللى انت عايزها ولتكن امريكا  هتنسخ رقم الاى بى يا معلم  وتنقل الرقم الأول الكبير فى خانةadress والصغير فى خانة port وتضغط ok وبكده مبروك عليك الاى بى الجديد . وتنقل الرقم الأول الكبير فى خانةadress والصغير فى خانة port وتضغط ok وبكده مبروك عليك الاى بى الجديد . لو عايز تتأكد ان الاى بى بتاعك اتغير تدخل الرابط ده هيظهر لك الاى بى بتاعك بعد التغيير وده دليل على ان مفيش حد يقدر يكشفك ip-adress.com  ياريت اكون افدتكم بفكرة جديدة انا عارف ان كتير منكم عارف الطريقة دى لكن عارف برده ان فى ناس كتير مش عارفة ومن حقها تتعلم..وعلى فكرة الطريقة دى أحسن من برامج تغيير واخفاء الاى بى اللى مليانة فيروسات وبتشل الجهاز زائد ان ممكن تلغى اللى انت عملته بمجرد ما تمسح الارقام للأى بى وتضغط ok وبكده انتهى الموضوع. |






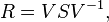

 can be diagonalized as
can be diagonalized as  and
and  .
.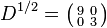 , giving the square root
, giving the square root 



 مدونة حلمنا
مدونة حلمنا مدونة ماي تكنولوجي
مدونة ماي تكنولوجي تقنيتي
تقنيتي برامج كوم
برامج كوم أساحبى كوميكس
أساحبى كوميكس  اسم المدونة
اسم المدونة المحترف الصغير ا
المحترف الصغير ا  كن محترف
كن محترف مدونة عماد الرافعي
مدونة عماد الرافعي






